Sorting algorithms are a fundamental part of computer science. Being able to sort through a large data set quickly and efficiently is a problem you will be likely to encounter on nearly a daily basis.
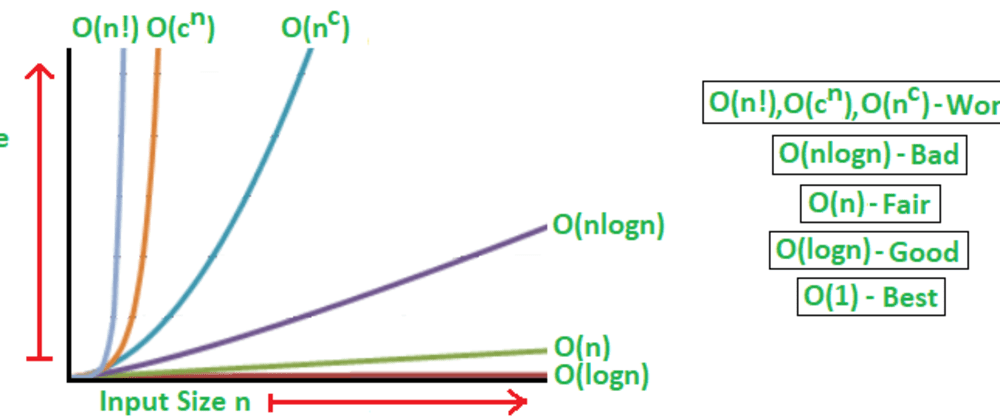
- In computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the length of the string representing the input. The time complexity of an algorithm is commonly expressed using big O notation, which excludes coefficients and lower order terms.
- Time complexity is a method for comparing the abstract time an algorithm takes to execute. It doesn't refer to actual time or duration. It is only useful for comparing (and in comparing the same discrete elements; not all algorithms have the same elements).
- Run time complexity is how many iterations an algorithm takes to solve a problem and space time is how much memory is needed. In modern computing, space is less of a concern so most algorithms.
Here are the main sorting algorithms:
| Algorithm | Data Structure | Time Complexity - Best | Time Complexity - Average | Time Complexity - Worst | Worst Case Auxiliary Space Complexity |
|---|---|---|---|---|---|
| Quicksort | Array | O(n log(n)) | O(n log(n)) | O(n^2) | O(n) |
| Merge Sort | Array | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(n) |
| Heapsort | Array | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(1) |
| Bubble Sort | Array | O(n) | O(n^2) | O(n^2) | O(1) |
| Insertion Sort | Array | O(n) | O(n^2) | O(n^2) | O(1) |
| Select Sort | Array | O(n^2) | O(n^2) | O(n^2) | O(1) |
| Bucket Sort | Array | O(n+k) | O(n+k) | O(n^2) | O(nk) |
| Radix Sort | Array | O(nk) | O(nk) | O(nk) | O(n+k) |
Efficiency of an algorithm depends on two parameters: 1. Time Complexity. Space Complexity. Time Complexity: Time Complexity is defined as the number of times a particular instruction set is executed rather than the total time is taken. It is because the total time taken also depends on some external factors like the compiler used, processor.
Another crucial skill to master in the field of computer science is how to search for an item in a collection of data quickly. Here are the most common searching algorithms, their corresponding data structures, and time complexities.

Here are the main searching algorithms:
| Algorithm | Data Structure | Time Complexity - Average | Time Complexity - Worst | Space Complexity - Worst |
|---|---|---|---|---|
| Depth First Search | Graph of |V| vertices and |E| edges | - | O(|E|+|V|) | O(|V|) |
| Breadth First Search | Graph of |V| vertices and |E| edges | - | O(|E|+|V|) | O(|V|) |
| Binary Search | Sorted array of n elements | O(log(n)) | O(log(n)) | O(1) |
| Brute Force | Array | O(n) | O(n) | O(1) |
| Bellman-Ford | Graph of |V| vertices and |E| edges | O(|V||E|) | O(|V||E|) | O(|V|) |

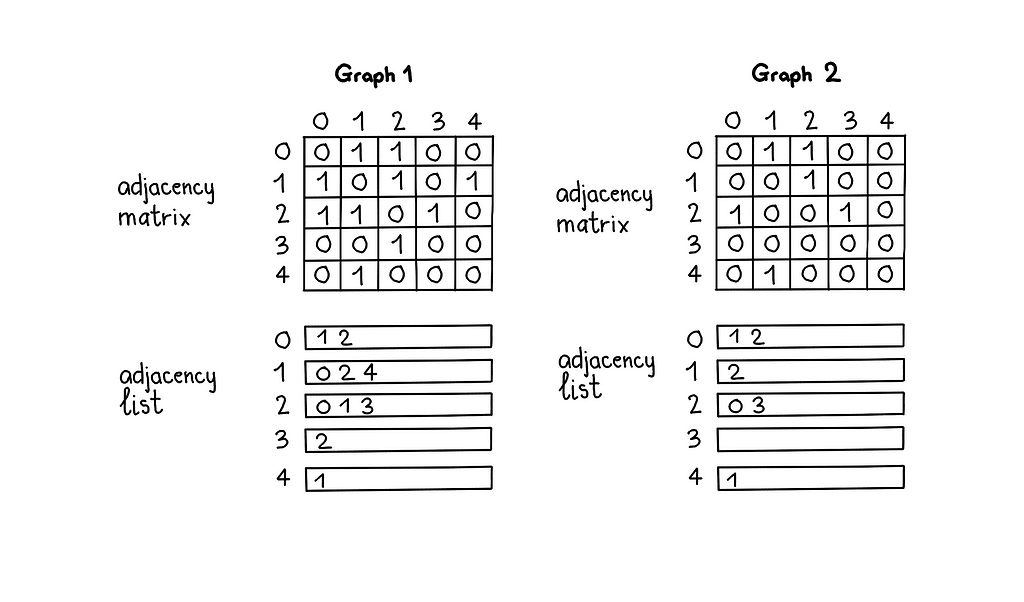
Graphs are an integral part of computer science. Mastering them is necessary to become an accomplished software developer. Here is the data structure analysis of graphs:
| Node/Edge Management | Storage | Add Vertex | Add Edge | Remove Vertex | Remove Edge | Query |
|---|---|---|---|---|---|---|
| Adjacency List | O(|V|+|E|) | O(1) | O(1) | O(|V| + |E|) | O(|E|) | O(|V|) |
| Incidence List | O(|V|+|E|) | O(1) | O(1) | O(|E|) | O(|E|) | O(|E|) |
| Adjacency Matrix | O(|V|^2) | O(|V|^2) | O(1) | O(|V|^2) | O(1) | O(1) |
| Incidence Matrix | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|E|) |
Storing information in a way that is quick to retrieve, add, and search on, is a very important technique to master. Here is what you need to know about heap data structures:
| Heaps | Heapify | Find Max | Extract Max | Increase Key | Insert | Delete | Merge |
|---|---|---|---|---|---|---|---|
| Sorted Linked List | - | O(1) | O(1) | O(n) | O(n) | O(1) | O(m+n) |
| Unsorted Linked List | - | O(n) | O(n) | O(1) | O(1) | O(1) | O(1) |
| Binary Heap | O(n) | O(1) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(m+n) |
| Binomial Heap | - | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) |
| Fibonacci Heap | - | O(1) | O(log(n))* | O(1)* | O(1) | O(log(n))* | O(1) |
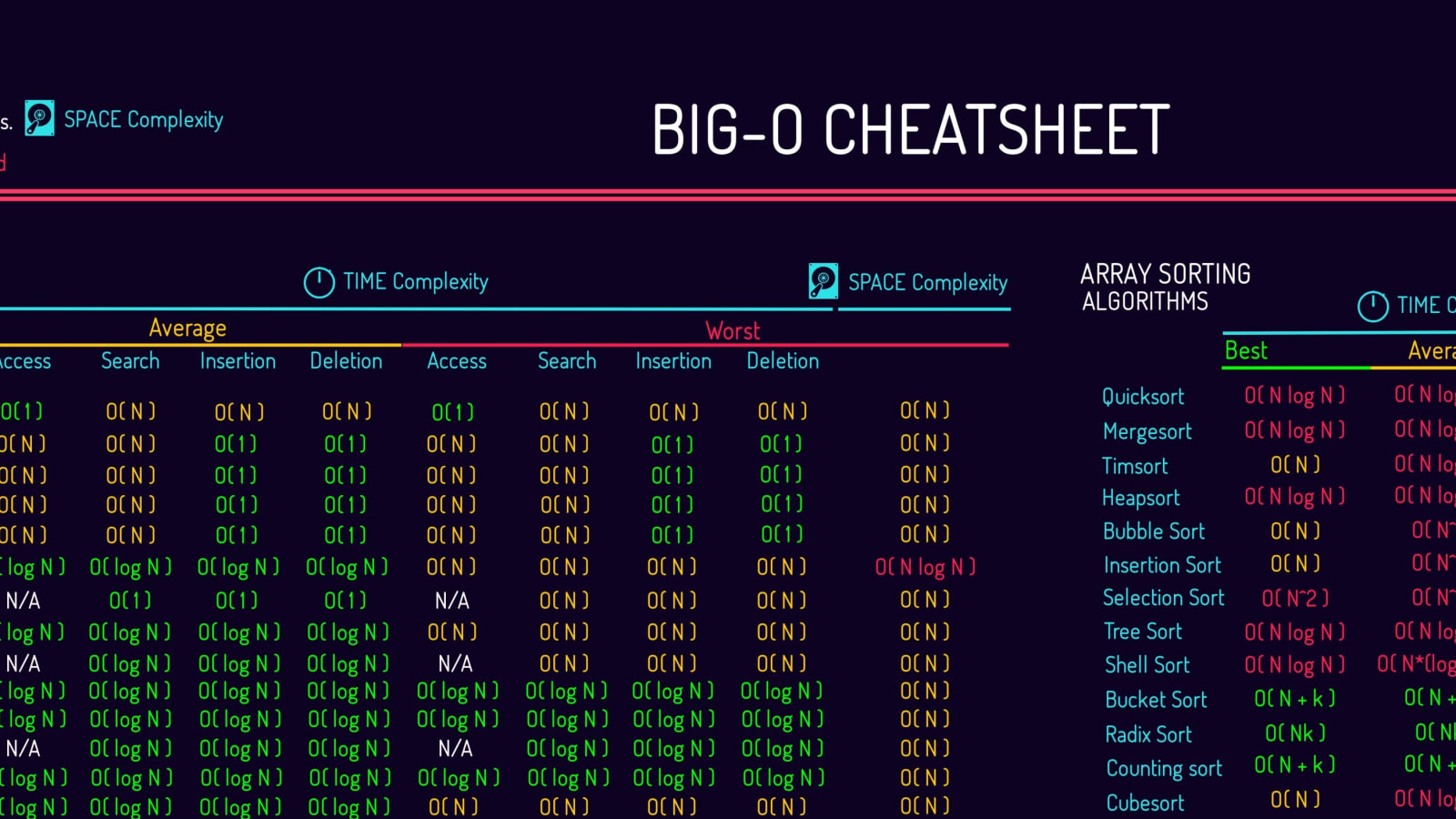
Common Data Structure Operations
| Data Structure | Time Complexity | Space Complexity | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Average | Worst | Worst | |||||||
| Access | Search | Insertion | Deletion | Access | Search | Insertion | Deletion | ||
| Array | Θ(1) | Θ(n) | Θ(n) | Θ(n) | O(1) | O(n) | O(n) | O(n) | O(n) |
| Stack | Θ(n) | Θ(n) | Θ(1) | Θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Queue | Θ(n) | Θ(n) | Θ(1) | Θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Singly-Linked List | Θ(n) | Θ(n) | Θ(1) | Θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Doubly-Linked List | Θ(n) | Θ(n) | Θ(1) | Θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Skip List | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n log(n)) |
| Hash Table | N/A | Θ(1) | Θ(1) | Θ(1) | N/A | O(n) | O(n) | O(n) | O(n) |
| Binary Search Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n) |
| Cartesian Tree | N/A | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | N/A | O(n) | O(n) | O(n) | O(n) |
| B-Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| Red-Black Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| Splay Tree | N/A | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | N/A | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| AVL Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| KD Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n) |
Array Sorting Algorithms
Time Complexity Of Algorithms Cheat Sheet Pdf
| Algorithm | Time Complexity | Space Complexity | ||
|---|---|---|---|---|
| Best | Average | Worst | Worst | |
| Quicksort | Ω(n log(n)) | Θ(n log(n)) | O(n^2) | O(log(n)) |
| Mergesort | Ω(n log(n)) | Θ(n log(n)) | O(n log(n)) | O(n) |
| Timsort | Ω(n) | Θ(n log(n)) | O(n log(n)) | O(n) |
| Heapsort | Ω(n log(n)) | Θ(n log(n)) | O(n log(n)) | O(1) |
| Bubble Sort | Ω(n) | Θ(n^2) | O(n^2) | O(1) |
| Insertion Sort | Ω(n) | Θ(n^2) | O(n^2) | O(1) |
| Selection Sort | Ω(n^2) | Θ(n^2) | O(n^2) | O(1) |
| Tree Sort | Ω(n log(n)) | Θ(n log(n)) | O(n^2) | O(n) |
| Shell Sort | Ω(n log(n)) | Θ(n(log(n))^2) | O(n(log(n))^2) | O(1) |
| Bucket Sort | Ω(n+k) | Θ(n+k) | O(n^2) | O(n) |
| Radix Sort | Ω(nk) | Θ(nk) | O(nk) | O(n+k) |
| Counting Sort | Ω(n+k) | Θ(n+k) | O(n+k) | O(k) |
| Cubesort | Ω(n) | Θ(n log(n)) | O(n log(n)) | O(n) |
